Newton's method, in very few lines of Haskell

I hesitate to even write this blog post, because when I saw the code, it seemed trivial. But then, maybe that's the best kind of code. I'm going to assume that you know about Newton's method for approximately solving equations of the form f(x) = 0. The short explanation is that you start out with a guess point, x₀, and then iterate from there with this equation:

This requires you to know the derivative of the function. Let's write this in Haskell:

next f f' xn = xn - ((f xn) / (f' xn))

Apply this to some starting number, and you get the next one. For example, suppose that you're trying to solve sin(x) = 0, and your starting guess is 3:

*Main> next sin cos 3
3.142546543074278

Now try applying it again a couple more times:

*Main> let iter = next sin cos
*Main> iter 3
3.142546543074278
*Main> iter (iter 3)
3.141592653300477
*Main> iter (iter (iter 3))
3.141592653589793
*Main> pi
3.141592653589793

After just three iterations, we get pi, correct to at least fifteen decimal places. Since this is Haskell, let's make a list of all the iterations:

newton f f' x0 = iterate next x0
    where next xn = xn - ((f xn) / (f' xn))

The iterate function takes a function f and an initial value x, and returns the list [x, f(x), f(f(x)), ...]. This is exactly what we need to express the iteration in Newton's method. Let's try it out:

*Main> take 4 $ newton sin cos 3
[3.0, 3.142546543074278, 3.141592653300477, 3.141592653589793]

Score! Let's try it out on a more complicated function, f(x) = 12x⁴ - 5x³. Here's what it looks like:

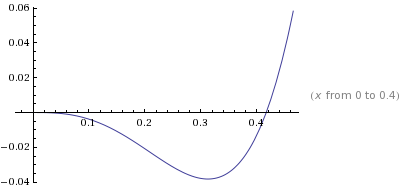
Let's see if we can find that root a little past x = 0.4, with some wild guess.

*Main> mapM_ print $ take 50 $ newton (\x -> 12*x^4 - 5*x^3) (\x -> 48*x^3 - 15*x^2) 400
400.0
300.02606202762576
225.04561534004728
168.81028938363653
126.63380700188723
95.00146134126632
71.2772236173846
53.48407405669417
40.13925026128285
30.130683698176643
22.62432736171233
16.994651928171486
12.772518440796631
9.606083627985576
7.231480047805808
5.4508278904529295
4.115746372269005
3.1149912022861663
2.365188920791852
1.8038979233235874
1.384421748669219
1.071949969695422
0.8407198212811359
0.6719880367106018
0.5526705013094125
0.47442889059722404
0.4321200911656781
0.4181639590095718
0.4166825795028489
0.4166666684895603
0.4166666666666667
0.41666666666666663
0.41666666666666663
...

Not bad! Starting it with an even higher guess doesn't hurt the speed much, either. So there you have it: Newton's method in two lines of Haskell code. I feel like there ought to be more to it, but there just isn't.

(A word about speed, in case you were wondering: the list construction will get optimized away, and this will turn into essentially the same compiled code as if you had written it in C. The compiler is allowed to be smart, sometimes.)